Wat is een statistiek? Een statistiek is een aantal of een hoeveelheid vergeleken met een eerder aantal of eerdere hoeveelheid van hetzelfde. Statistieken hebben betrekking op de hoeveelheid werk die gedaan is of de waarde ervan uitgedrukt in geld.

Een neerwaartse statistiek betekent dat de huidige hoeveelheid lager ligt dan zij eerder lag.

Een opwaartse statistiek betekent dat de huidige hoeveelheid hoger ligt dan zij eerder lag.

We werken op basis van statistieken. Deze laten zien of een medewerker of groep al dan niet werkt, omdat het werk de statistiek voortbrengt. Als hij niet effectief werkt, gaat de statistiek onvermijdelijk naar beneden. Als hij wel effectief werkt, gaat de statistiek omhoog.

Negatieve Statistieken

Sommige dingen gaan statistisch gezien omhoog terwijl ze slecht zijn (zoals auto-ongelukken). We gebruiken echter geen negatieve statistieken. We gebruiken alleen dingen die iets positiefs betekenen wanneer ze omhooggaan of iets negatiefs wanneer ze omlaaggaan.

Grafische Voorstellingen van Statistieken

Een grafiek is een lijn of diagram waarbij die lijn of dat diagram laat zien hoe een hoeveelheid afhankelijk is van, vergeleken wordt met, of verandert ten opzichte van een andere hoeveelheid. Het is iedere grafische voorstelling die wordt gebruikt om een numeriek verband te laten zien.

Een grafiek levert onvoldoende informatie op als de verticale schaalverdeling zodanig is, dat de veranderingen in de lijn van de grafiek te klein zijn. Wanneer de veranderingen in de lijn te groot zijn, is het natuurlijk überhaupt onmogelijk om de grafiek te tekenen.

Als de stijgingen en dalingen niet duidelijk op een grafiek zichtbaar zijn, dan zullen degenen die de grafiek interpreteren fouten maken. Wat er dan bijvoorbeeld als een vlakke lijn uitziet, zou er eigenlijk als een bergketen uit moeten zien.

Met schaalverdeling wordt het aantal van iets per verticale centimeter op de grafiek bedoeld.

De schaalverdeling wordt op de volgende manier bepaald:

De schaalverdeling is voor elke statistiek anders.

1. Stel vast wat de kleinste hoeveelheid van een bepaalde statistiek naar verwachting zal bedragen – dat hoeft niet altijd nul te zijn.

2. Stel vast wat de grootste hoeveelheid is die men in de volgende drie maanden op de statistiek denkt te kunnen behalen.

3. Trek (1) van (2) af.

4. Zet de uitkomst van (3) gelijkmatig uit op de verticale as.

Je schaalverdeling zal dan heel realistisch zijn en de stijgingen en dalingen goed weergeven.

Grafische Voorstellingen van Statistieken
Een grafiek met een incorrecte schaalverdeling toont de veranderingen in de statistiek niet exact en maakt daarmee de grafiek dus minder bruikbaar.	Een grafiek met een correcte schaalverdeling toont overduidelijk de veranderingen in een statistiek, waardoor het gemakkelijker wordt om vast te stellen welke conditie moet worden toegepast.

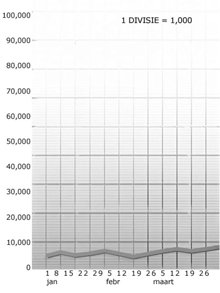
Hier volgt een onjuist voorbeeld.

Laten we een organisatie nemen die 5000 euro per week omzet. We delen de verticale streepjes van het grafiekpapier, waarvan er 100 zijn, zodanig in dat elk streepje 1000 euro voorstelt. Als dit in een grafiek wordt uitgezet, zal dat een lage, nogal vlakke lijn te zien geven, ongeacht hoe de inkomsten van de organisatie ook variëren, en dus geen aandacht van leidinggevenden trekken wanneer de statistiek stijgt of daalt.

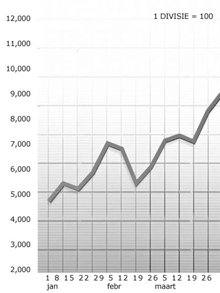
Hier volgt de juiste aanpak om de schaalverdeling te bepalen voor het Bruto Inkomen van een organisatie wanneer dat gemiddeld 5000 euro per week bedraagt.

1. Als we de oude grafieken van de laatste 6 maanden bekijken, zien we dat de inkomsten nooit onder de 2400 euro zijn gekomen. Dus nemen we 2000 euro als het laagste punt op het grafiekpapier.

2. We schatten dat deze organisatie in de volgende drie maanden af en toe 12.000 euro moet kunnen halen. Daarom zetten we dat bovenaan het grafiekpapier.

3. We trekken 2000 euro van 12.000 euro af en we komen dan op 10.000 euro uit.

4. We gaan uit van 100 verticale vakjes en maken elk 100 euro, beginnend met 2000 euro bij het laagste streepje.

Nu zetten we het Bruto Inkomen in de grafiek uit met 100 euro per streepje van de schaalverdeling.

Dit zal een juist beeld geven en duidelijk de stijgingen en dalingen laten zien en daardoor zal de grafiek voor leidinggevenden bruikbaar zijn bij het interpreteren ervan.

Probeer gemakkelijke rekeneenheden te gebruiken, zoals 5, 10, 25, 50 of 100, en geef de schaalverdeling op de grafiek aan (bijv. 1 eenheid = 25).

Het element hoop kan in een grafiek te sterk naar voren komen. Men hoeft geen schaalverdeling te berekenen voor meer dan één grafiek tegelijk. Als je op een nieuw vel grafiekpapier overgaat, bereken dan de schaalverdeling helemaal opnieuw; naarmate de activiteit in de organisatie toeneemt, kan de schaalverdeling per vel worden bijgesteld. Zo kostte het bijvoorbeeld eens 18 maanden om de statistieken van één organisatie met een factor 5 omhoog te krijgen (5 maal zoveel inkomen, enz.) en daarvoor was natuurlijk een aantal vellen grafiekpapier nodig. Laat de schaal dus niet verdergaan dan wat op dat moment de verwachtingen zijn.

Probeer de horizontale tijdschaal niet meer dan 3 maanden te laten beslaan. Men kan die schaal namelijk ook te veel gaan samenpersen. Daarentegen kan men haar ook te veel spreiden, waardoor de grafiek er weer als een vlakke lijn gaat uitzien en niet de juiste informatie zal weergeven.

Het vaststellen van de juiste schaalverdeling is de essentie van het maken van goede grafieken.